How to Test for the Underlying Assumptions of Linear Regression?

Regression analysis is a versatile and powerful tool. However, it is also misused and abused due to insufficient understanding of the regression theory. One source of error is the unawareness of the assumptions underlying regression models. Regression analysis is built on four assumptions. Ideally, these assumptions must be true to use the regression model to make inferences or predictions. If these assumptions are not true, your regression model could be incorrect, biased, or misleading. You must either 1) fix the model using data transformations or 2) seek alternative frameworks and tests to evaluate your data and make inferences or predictions. This page outlines what we emphasize when we tutor regression analysis to our students.

What are Underlying Assumptions of Regression Analysis?

So what are the assumptions that underlie regression analysis? The regression model is built on four assumptions:

  1. Linearity: There is a linear relationship between the independent and dependent variables.
  2. Independence: The regression errors are independent.
  3. Normality: The errors are normally distributed.
  4. Equal variance or homoscedasticity: The errors have equal or constant variance.

We can sum up these assumptions in a single sentence: the regression errors are independent and are normal random variables with a mean of zero and constant variance.

Why is it Important to Understand the Assumptions of Regression Analysis?

You evaluate your regression model before you make inferences or predictions. And part of evaluating your regression model is knowing and testing if the underlying assumptions of regression analysis hold true. Therefore, it is important to understand the underlying assumptions of regression analysis and modeling.

You should generally NOT use the regression model to make inferences or predictions if the underlying assumptions of regression analysis are not met. Instead, seek out other tests to understand the data and relationships you are seeking.

Can we use the Regression Model if the Underlying Assumptions of Regression Analysis are not met? If Yes, When?

Hypothesis tests and confidence intervals for the intercept and coefficients are quite forgiving even if your regression model does not meet the normality test. This is the only occasion when it may be OK to use regression analysis when the underlying assumptions of regression analysis are not met.

The tests and prediction intervals are sensitive to departures from the other assumptions (equal variance, independence, and linearity).

What Happens if my Model’s Underlying Assumptions of Regression Analysis are not met?

You can fix the model in several ways if the underlying assumptions of regression analysis are not met. For example, you may need to segment the data into different batches or eliminate outliers; you may want to transform the data in different ways (squaring, logs, etc.)

If these modifications to the model and data do not meet the underlying assumptions, you must seek alternative frameworks and tests to evaluate your data and make inferences or predictions.

OK, So now that I understand that it is essential to test the underlying assumptions of regression analysis, what do I need to do to test if the underlying assumptions are met?

What do I need to Test the Underlying Assumptions of Regression Analysis?

Each of the four underlying assumptions of a regression model can be checked separately using the following tools.

  1. Linearity: X vs. Y scatter plots, observed vs. predicted values plot, various residual plots including residuals vs. fitted values, residuals vs. independent variables, and residuals vs. transformations;
  2. Independence: Residuals in sequence or order or time
  3. Normality: histogram, box plots, normal probability plot
  4. Equal variance or homoscedasticity: Residual plots – residuals vs. fitted values, independent variables, and time if it is a time series

Testing the Underlying Assumptions of Regression Analysis Using Excel’s Regression Tools?

Most statistical packages allow you to run regression models and test the underlying assumptions of regression models. However, we will discuss how you can test the underlying assumptions of regression models using Microsoft Excel as it is ubiquitous. Microsoft Excel’s regression outputs can be used to test the underlying assumptions of a regression model.

Testing for Linearity in a Regression Model Using Microsoft Excel’s Regression Output.

The Line Fit Plot allows you to check the linearity assumption in a regression model (top right).

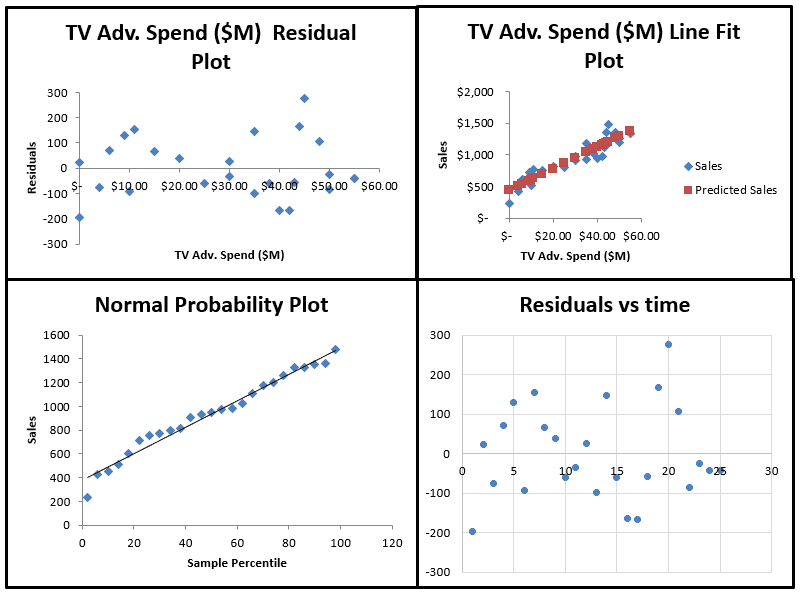
Microsoft Excel’s Regression Plots

You want to see the observed values spread evenly around the predicted values line in the line fit plot.

Testing for Independence in a Regression Model Using Microsoft Excel’s Regression Output.

Microsoft Excel’s regression residual plot plots the independent variable on the x-axis and the residuals on the y axis. You can use this residual plot to test for the independence assumption in a regression analysis.

Testing for Normality in a Regression Model Using Microsoft Excel’s Regression Output

Microsoft Excel’s regression output gives you a normal probability plot. The normal probability plot is a classic way to check the normality assumption. The normal probability plot has percentiles on the x-axis and the dependent variable values on the y-axis. If the normal probability plot gives you a fairly straight line along the diagonal, you can be assured that the normality assumption is being met. If the values deviate from a string line, the underlying data is not normal – either tails are too fat, or short or data are skewed.

You can see some excellent examples on the ITL NIST website.

Testing for Equal Variance in a Regression Model Using Microsoft Excel’s Regression Output

Microsoft Excel’s regression residual plot plots the independent variable in the x-axis and the residuals on the y axis. This allows you to test for equal variance in the underlying model. You want to see an even dispersion of residual errors above and below the line. Any noticeable patter is a violation of the equal variance assumption.

Fixing a Regression Model

Now you know how to test if the underlying assumptions of a regression model have been violated! What do you do if the underlying assumptions of a regression model have been violated? We discuss how you fix the regression model when each of the underlying assumptions of a regression model have been violated below.

How to fix the Regression Model if the Linearity Assumption Is Broken?

Linearity – or the assumption that the expected value of the dependent variable and independent variables have a linear relationship a fundamental assumption of regression modeling. So a violation of the linear assumption is a very serious assumption making the model questionable. If the linearity assumption is not met, you can try to fix the regression model by transforming the x and or y variables. These transformations include logarithms (natural or other base), squaring, cubing, etc. Another variable’s impact may also cause the non-linearity. So understanding the data and thinking about the possible causes is another way to fix the regression model if the linearity assumption is violated.

How to fix the Regression Model if the Independence Assumption (also called Autocorrelation) is Broken?

The independence or statistical independence of the errors is an essential assumption in building a regression model. Independence of statistical independence of the errors means that residual errors are independent of each other. In other words, independence means that there is no correlation between consecutive residual errors of a regression model. There should not be any correlation between consecutive errors; however, they are arranged. This is also referred to as autocorrelation in statistical forecasting textbooks.

If the independence assumption is broken, we know that the model needs to be revised/fixed. Differencing is usually the first step. Other revisions to the regression model include adding lags, accounting for the seasonal or cyclical factors, reviewing the differencing if you have overdone the differencing, etc. You may also want to stationarize and or standardize the data and try again.

How to fix the Regression Model if the Normality Assumption is Broken?

Most regression texts have normality of errors as an assumption in building the regression model – not all! This is because if we are not estimating the confidence intervals, and we are only interested in estimating coefficients, we can ignore the normality assumption. When the underlying data is not normally distributed, it is likely skewed to one side. This causes the parameters to get biased, leaving the regression model less than ideal. Also, remember – only the prediction errors need to be normally distributed.

What happens if the normality assumption is broken? If the normality assumption is violated, we can fix the regression model by examining the data carefully. Removing outliers may fix the issue. Sometimes transforming the x and or y variables are required to fix the normality of errors assumption. Sometimes it may require the data to be broken into two or more separate parts as they have clearly distinct impact.

How to Fix the Regression Model if the Homoscedasticity (Constant Variance) of Errors Assumption is Broken?

The assumption of constant variance of errors, also called homoscedasticity of errors, can be spotted by looking at the residual plots. If this assumption is not held to be true, the standard errors become unreliable leading to poor confidence interval estimates. A violation of the homoscedasticity assumption is also referred to as heteroscedasticity.

Often heteroscedasticity or a violation of the homoscedasticity assumption in regression is due to inflation or compound growth in the variables. Log transformation or deflating the variables can fix this issue. If this violation is due to inflation or compound growth in the variables, your residual plots will reflect patterns.

Sometimes, heteroscedasticity or a violation of the homoscedasticity assumption in regression is due to seasonal patterns. Here too, log transformation or deflating the variables may fix this issue. Using dummy variables for seasons must also be tried and often fixes issues due to seasons.

More Resources to learn about the Underlying Assumptions of Linear Regression

Here are some resources to learn more about testing the underlying assumptions of linear regression and how to fix any issues you find.

Art or Science? Testing the Underlying Assumptions of Linear Regression?

Testing for the underlying assumptions of linear regression can seem complicated. There is some judgment required. Students gain confidence as they practice testing the assumptions of regression modeling and examining more regression output plots. Feel free to email or call us if we can help you with regression analysis tutoring.

Sign Up Now