Estimating the Sample Size Required for a Target Margin of Error (MoE)

The Need for a Margin of Error

We are often limited to sample data when making decisions. However, we know that the sample statistics, such as the mean, will vary each time I take a sample. Therefore, we know it has an error which we refer to as a sampling error. We compensate for this error by not limiting ourselves to the sample mean, which is a single-point estimate. Instead, we seek a range of values – above and below the sample mean, that we believe will contain the true population mean.  This range above or below the mean is called the margin of error.

How wide should the Margin of Error be?

We understand that there will be sampling errors. How much of an error are you willing to tolerate? In other words, how wide should the margin of error be? The width of the margin of error is based on the following:

  1. Alpha or α, which is the risk of rejecting a true hypothesis or Type 1 error,
  2. Power or β, which is the risk of accepting a false null hypothesis or Type 2 error and
  3. The population standard deviation.

Which of the above factors gets priority will depend on the nature of the data. There will be tradeoffs in setting the margin of error. 

Derivation of the Sample Size formula. 

Derivation of the sample size formula starts with the Confidence interval formula or the margin of error.

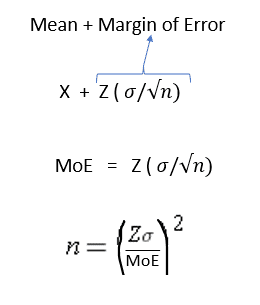
As you can see from the formula, the margin of error depends on 

  • The standard deviation;
  • The sample size; and 
  • Confidence level we seek.

Each of these three factors impacts the margin of error in different ways. 

  • The standard deviation: the larger the standard deviation, the larger the margin of error.
  • The sample size: the larger the sample size, the larger the margin of error.
  • Confidence level we seek: Larger the confidence level, the larger the margin of error.

Surveyors and samplers want to of course, limit the margin of error. They cannot force a change in the population standard deviation. However, they do not want to lower their confidence level either. So the only factor that impacts the margin of error that samplers can control is the sample size. This leads to the question:

How large a sample do we need to achieve a target Margin of Error?

This question is addressed using these formulas based on if we are working with a mean or proportion!

Sign Up Now