All MBA and CFA students encounter the time value of money concept early in their finance programs. Many students are troubled by the interest rates given in different formats and the compounding frequency in their first few weeks. This article addresses the common terms, challenges and questions.
- What is The Annual Percentage Rate (APR)
- When is The Annual Percentage Rate (APR) Irrelevant?
- How is The Annual Percentage Rate (APR) Adjusted to Account for Compounding?
- EAR with Semi-Annual Compounding
- EAR with Quarterly Compounding
- What is The Effective Annual Rate (EAR)?
- What is The Formula for Effective Annual Rate (EAR)?
- What is the formula for APR?
What is The Annual Percentage Rate (APR)
The annual percentage rate (APR) is the stated interest rate or annual rate if the interest is computed once a year.
For example, if you borrow $100 at a rate of 12% per annum, the APR is 12%. This is often simply stated as an interest rate of 12% annually. Here, you will pay $112 to repay the loan and interest at the end of the year.
When is The Annual Percentage Rate (APR) Irrelevant?
Lenders often charge interest on a non-annual basis. In these cases, your principal increases by the interest earned in the period, and your next period’s interest is higher than the interest of the preceding period. Those cases where interest is computed on a non-annual basis is known as compounding in finance.
We should not use the APR to compute interest when interest is compounded. We adjust the APR to reflect the increased frequency of interest calculations.
How is The Annual Percentage Rate (APR) Adjusted to Account for Compounding?
When there is a compounding of interest, the APR needs to be adjusted to account for the compounding effect. The APR is adjusted by dividing the APR by the number of compounding periods in a year. For example, if the compounding happens twice a year, you will divide the APR/2 to get the interest rate semi annually. if the compounding happens quarterly, you will divide the APR by 4 to get the interest rate quarterly.
EAR with Semi-Annual Compounding
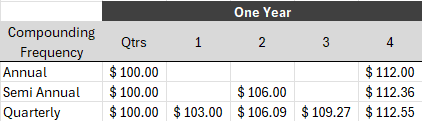
For example, if you borrow $100 at an interest rate of 12% per annum compounded semi-annually, the APR is 12%. However, because the interest is computed every six months, you will pay more than $112 to repay the loan and interest at the end of the year.
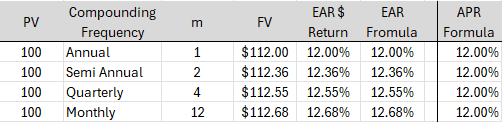
At the end of six months, your principal and interest become $100*(1+12%/2)=$106. So, for the second six months, the principal is $106, which is higher than the $100 you started with. So the loan and interest at the end of the year are $106*(1+12%/2)=$112.36. This is higher than the $112 you had to repay when interest was computed annually. Your EAR is 12.36% vs. 12% APR!
EAR with Quarterly Compounding
Take another example with quarterly compounding. If you borrow $100 at an interest rate of 12% per annum compounded quarterly, the APR is 12%. However, because the interest is computed every three months, you will pay more than $112 to repay the loan and interest at the end of the year.
At the end of three months, your principal and interest becomes $100*(1+12%/4)=$103. So for the second three-month period, the principal is $103, which is higher than the $100 you started with. So, the loan and interest at the end of the second quarter is $103*(1+12%/4)=$106.09. At the end of the third quarter, the loan and interest amount to $106.09*(1+12%/4)=$109.27. Finally, at the end of the fourth quarter or the end of the year, the loan and interest you must pay is $109.27*(1+12%/4)=$112.55! This is higher than the $112 you had to repay when interest was computed annually or the $112.36 you had to repay when interest was computed semi-annually. When interest is computed quarterly, your EAR is 12.55% vs. 12% APR!
What is The Effective Annual Rate (EAR)?
The effective annual rate is the effective rate of interest you pay when interest is computed on a non-annual basis. In other words, if interest is computed semi annually or quarterly or monthly, the interest you pay is more than the stated APR. The effective rate of interest you pay when interest is computed is known as the EAR.
What is The Formula for Effective Annual Rate (EAR)?
The formula for effective annual rate (EAR) is :
EAR = (1+APR/m)^m – 1
- Where:
- m is the compounding frequency
- APR is the Annual Percentage Rate
- EAR is the Effective Annual Rate
Gotcha Questions?
Often students make a mistake in using the APR to do the compounding calculations. You have to watch out for words such as compounded monthly or semi annually or quarterly along with the stated APR or simply interest rate.
On rare occasions, interest rates specified as EAR or simply mentioned as effective rate are x! In these cases, you have to calculate the APR and then divide it by the compounding frequency to get the right interest rates.
What is the formula for APR?
One of the subtle gotcha questions professors drop is to give you the EAR. If students are not careful, they end up assuming that the EAR is the APR and get the answer wrong.
If you are given the EAR, what is the formula for APR? The formula for APR, if you are given the effective annual rate (EAR), is :
APR = (((1+EAR)^(1/m))-1)*m
- Where
- m is the compounding frequency
- EAR is the Effective Annual Rate
- APR is the Annual Percentage Rate
In the able above, we have computed the APR from the EAR using the above formula. Try it for yourself.